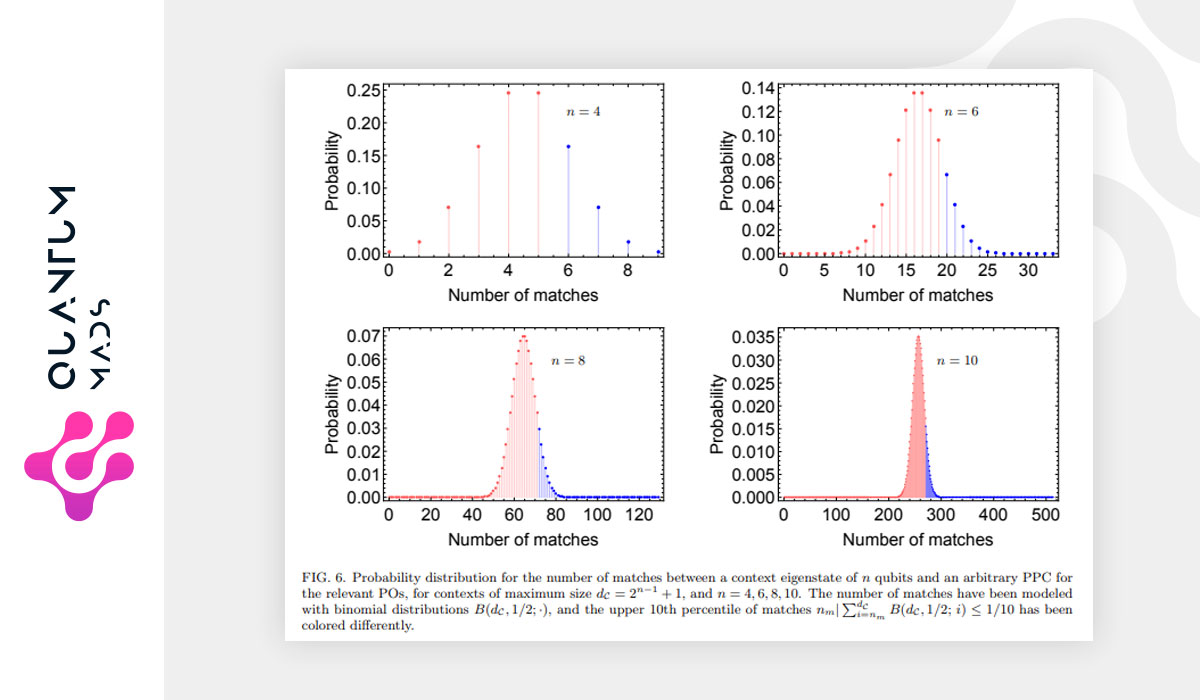
We propose a protocol to encode classical bits in the measurement statistics of a set of parity observables, leveraging quantum contextual relations for a random access code task. The intrinsic information redundancy of quantum contexts allows for a posterior decoding protocol that requires few samples when encoding the information in a set of highly entangled states, which can be generated by a discretely-parametrized quantum circuit. Applications of this protocol include algorithms involving storage of large amounts of data but requiring only partial retrieval of the information, as is the case of decision trees. This classical-to-quantum encoding is a compression protocol for more than 18 qubits and shows quantum advantage over state-of-the-art information storage capacity for more than 44 qubits. In particular, systems above 100 qubits would be sufficient to encode a brute force solution for games of chess-like complexity.
- Enhanced performance: a large amount of data can be compressed into few quantum resources
- Flexible applicability: any data can be strongly compressed as long as only part of it requires posterior consulting, making this ideal for decision tree compression
- Improved security: data can be sent with an unbreakable query limit
Read the whole article on arXiv