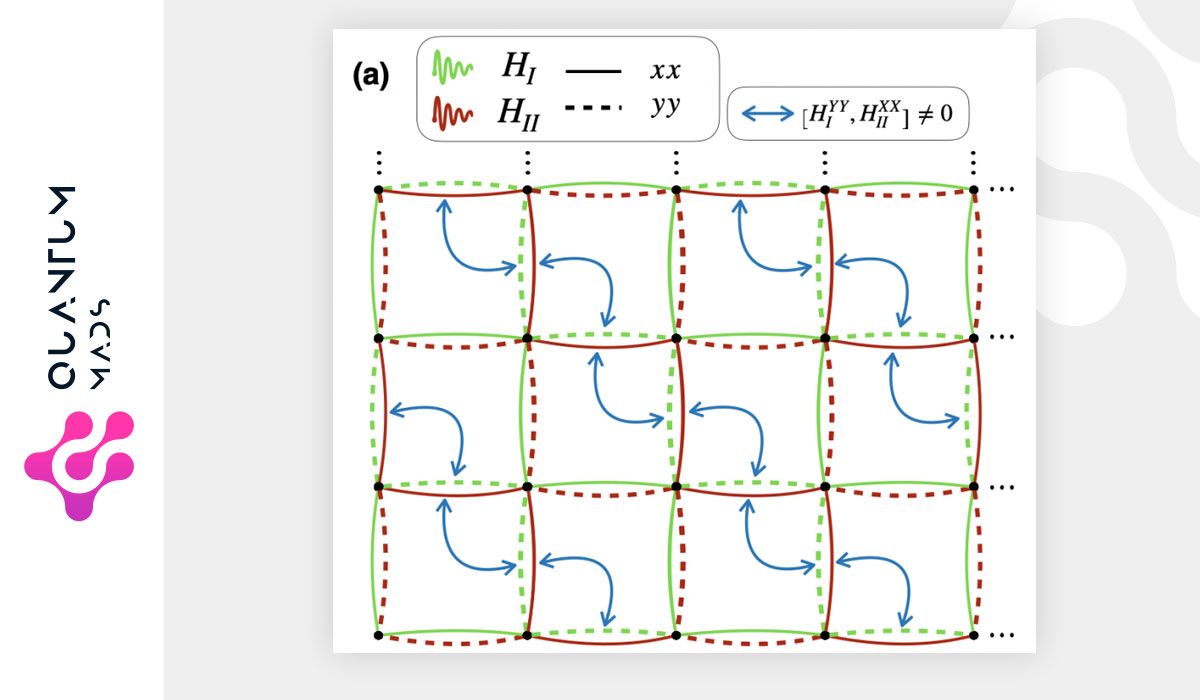
We consider superconducting architectures and extend the cross-resonance effect, up to first order in perturbation theory, from a two-qubit interaction to an analog Hamiltonian acting on one-dimensional (1D) chains and two-dimensional (2D) square lattices, which, in an appropriate reference frame, results in a purely two-local Hamiltonian. By augmenting the analog Hamiltonian dynamics with single-qubit gates we show how one may generate a larger variety of distinct analog Hamiltonians. We then synthesize unitary sequences, in which we toggle between the various analog Hamiltonians as needed, simulating the dynamics of Ising, XY, and Heisenberg spin models. Our dynamics simulations are Trotter error-free for the Ising and XY models in 1D. We also show that the Trotter errors for 2D XY and 1D Heisenberg chains are reduced with respect to a digital decomposition by a constant factor. We conclude with a discussion of how the Hamiltonian toggling techniques could be extended to derive new analog Hamiltonians, which may be of use in more complex digital-analog quantum simulations for various models of interacting spins.
Read the whole article on Physical Review journal