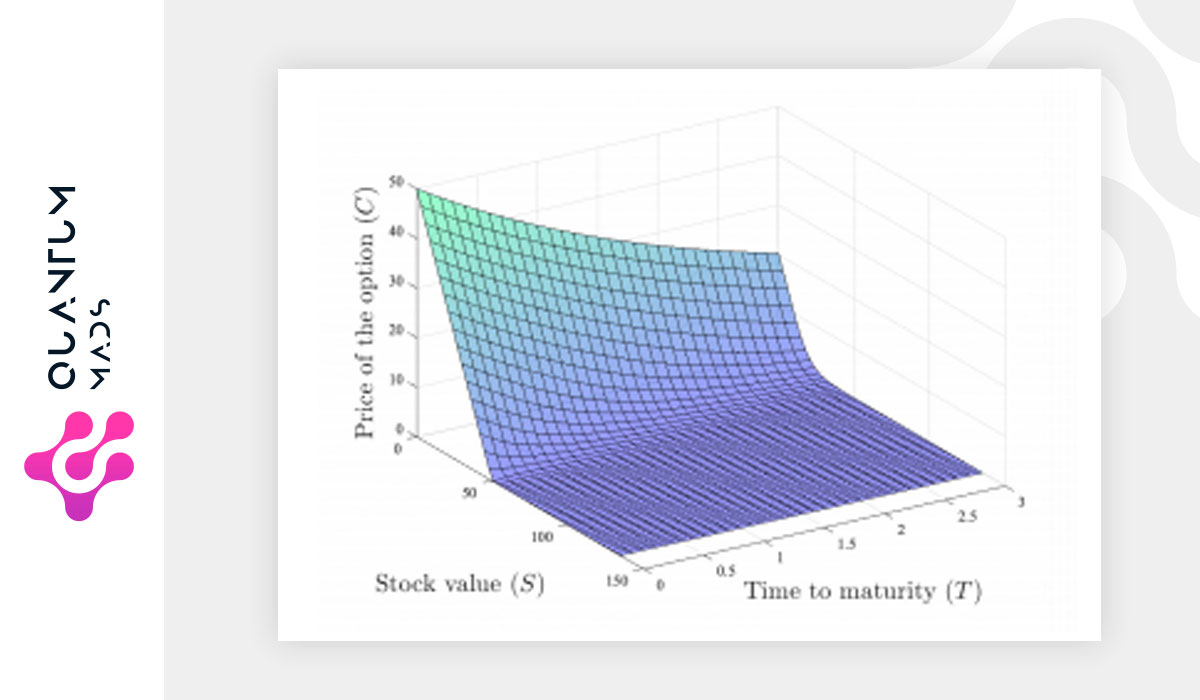
Pricing financial derivatives, in particular European-style options at different time-maturities and strikes, is a relevant financial problem. The dynamics describing the price of vanilla options when constant volatilities and interest rates are assumed, is governed by the Black-Scholes model, a linear parabolic partial differential equation with terminal value given by the pay-off of the option contract and no additional boundary conditions. Here, we present a digital quantum algorithm to solve Black-Scholes equation on a quantum computer for a wide range of relevant financial parameters by mapping it to the Schrödinger equation.
The non-Hermitian nature of the resulting Hamiltonian is solved by embedding the dynamics into an enlarged Hilbert space, which makes use of only one additional ancillary qubit. Moreover, we employ a second ancillary qubit to transform initial condition into periodic boundary conditions, which substantially improves the stability and performance of the protocol. This algorithm shows a feasible approach for pricing financial derivatives on a digital quantum computer based on Hamiltonian simulation, technique which differs from those based on Monte Carlo simulations to solve the stochastic counterpart of the Black Scholes equation. Our algorithm remarkably provides an exponential speedup since the terms in the Hamiltonian can be truncated by a polynomial number of interactions while keeping the error bounded.
We report expected accuracy levels comparable to classical numerical algorithms by using 10 qubits and 94 entangling gates on a fault-tolerant quantum computer, and an expected success probability of the post-selection procedure due to the embedding protocol above 60%.
Read the whole article on arXiv